Article sur les échangeurs thermiques

Cet article a été rédigé par le GRETh pour l'encyclopédie de l'énergie : http://encyclopedie-energie.org/

Dans le contexte énergétique actuel, la hausse des prix de l’énergie et la raréfaction des sources d’énergies fossiles poussent la société industrielle contemporaine à devenir de plus en plus performante aussi bien sur l’aspect financier et environnemental que sur l’aspect maitrise de l’énergie. Ce dernier point essentiel aujourd’hui, conduit les industriels dans une recherche des meilleurs rendements de leurs processus et une baisse de leur consommation énergétique devenus indispensables. L’objectif de performance énergétique par la maitrise et la rationalisation de l’énergie pour une meilleure efficacité passe en particulier par l’optimisation des différents organes process. Cette nouvelle stratégie de performance énergétique n’est pas seulement judicieuse du point de vue de l’écologie ou de l’énergie, elle est souvent très rentable pour de nombreux cas, voire même pour des installations de taille réduite. Cette rentabilité impose néanmoins une gestion minutieuse dans les petits systèmes, davantage encore que dans les grandes installations. À partir d’une situation bien définie, la rentabilité ne peut être garantie que par le recours à des solutions techniques optimales offrant le meilleur rendement possible par une gestion dynamique des systèmes. C’est là qu’intervient encore, et ceci depuis toujours, l’échangeur de chaleur. Celui-ci est un élément essentiel de la stratégie de performance énergétique.

Sans conteste l’échangeur de chaleur (ou échangeur thermique) occupe une place primordiale et indispensable dans tous les systèmes thermiques, qu’il soit pour un usage industriel (chimie, pétrochimie, sidérurgie, agroalimentaire (IAA), production d’énergie), pour l’automobile, l’aéronautique, le bâtiment résidentiel ou tertiaire…etc. De manière générale, on s’accorde à dire que plus de 90% de l’énergie thermique utilisée dans les procédés industriels transite au moins une fois par un échangeur de chaleur. [3]

Dans cette notice, nous aborderons les principales fonctions qu’un échangeur thermique peut assurer, les principales technologies et les méthodes de dimensionnement. Nous verrons que le choix et le dimensionnement d’un échangeur de chaleur, pour une application donnée, dépend de nombreux paramètres tels que : les propriétés physiques des fluides, leur agressivité, les températures ainsi que leur pressions de service, les matériaux…etc. Les contraintes d’encombrement et de maintenance doivent également être prises en compte, ainsi que les considérations économiques. Aussi, en fin de cette notice, on s’attache à fournir un listing des principaux logiciels de dimensionnement, des principaux fabricants d’échangeurs et organismes liés à ce composant.

NB : Dans cette notice, on se préoccupe des échangeurs de chaleur dit pariétal, c'est-à-dire ceux dont le fluide chaud et le fluide froid sont séparés par une paroi, généralement métallique. L’autre catégorie d’échangeur dit à contact direct occupe une place importante dans certaines applications spécifiques et nous renvoyons le lecteur à la référence [10] et [11] pour plus d’informations à ce sujet.

Tout au long de la lecture de cette notice, le lecteur pourra se référer à la nomenclature et aux références en fin de notice.

1. Principal but et fonction d’un échangeur thermique

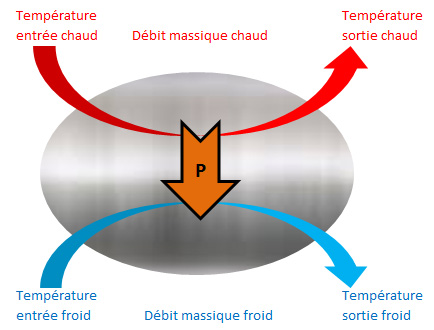
La fonction principale de l’échangeur thermique est de transférer de l’énergie thermique d’un fluide vers un autre à des niveaux de températures distincts.

Les fonctionnalités des échangeurs thermiques sont extrêmement diverses et variées. On peut, entres autres, citer les principales fonctionnalités suivantes [1]:

• Préchauffeur ou refroidisseur d’un liquide ou d’un gaz (air par exemple) pour lesquels de très nombreux exemples pourraient être rappelés et qui se caractérise par une fonction simple : le contrôle de la température du fluide en un point particulier du procédé ;
• Récupérateur thermique qui permet d’introduire la récente notion de valorisation de l’énergie thermique d’un procédé. La fonction de cet échangeur est alors d’assurer le transfert d’une capacité thermique maximale afin de permettre une valorisation maximale du rejet thermique sur des critères énergétiques et économiques ;
• Réfrigérants (et aéro-réfrigérant lorsque le vecteur de refroidissement est l’air, réfrigérant sur eau…) qui assure la dissipation de l’énergie thermique non valorisable d’un procédé vers le milieu extérieur – fonction essentielle dans de nombreux process ;
• Capteurs ou émetteurs thermiques dont les équipements ont pour fonction, respectivement, d’associer réception d’énergie thermique et transmission vers l’usage. Les exemples les plus courants sont les capteurs solaires thermiques ainsi que les radiateurs domestiques (qui assurent le confort thermique dans un bâtiment) ;
• Déshumidificateurs ou condenseurs partiels qui assurent la condensation d’une vapeur en mélange avec un gaz incondensable pour obtenir, en fin d’opération, un gaz appauvri en vapeur : l’exemple rencontré fréquemment est le déshumidificateur d’air humide qui permet d’assurer un contrôle de l’humidité de l’air en sortie de CTA (Centrale de Traitement d’Air). D’autres exemples industriels peuvent être cités comme la captation de vapeurs organiques dans les cryo-condenseurs ou les condenseurs de buées fréquemment rencontrés dans les installations de génie chimique ;
• Évaporateurs qui assurent l’évaporation complète ou partielle d’un liquide dans différents procédés notamment de production d’énergie mécanique (cycle moteur de Rankine, de Hirn) et de production frigorifique (cycle à compression (PAC), réfrigérateur…etc.) ;
• Condenseurs qui assurent la condensation complète ou partielle d’un gaz (vapeur) là encore par exemple pour la production d’énergie mécanique et frigorifique ;
• Équipements qui permettent la congélation et la fusion d’une phase liquide ou vapeur grâce à une paroi refroidie en dessous du point triple du fluide. Ces dispositifs sont utilisés pour assurer la séparation de plusieurs corps, assurer le stockage d’énergie thermique (stockage de glace ou stockage par MCP), produire une phase solide pour divers usages ;
• Le caloduc (Heat Pipe), véritable système thermique diphasique, qui permet notamment d’assurer la dissipation de la chaleur générée par les éléments électroniques (Microprocesseur, électronique embarquée…etc.), la récupération d’énergie, le maintien en température stable et uniforme…etc. Pour plus d’informations sur les caloducs vous pouvez vous référer à [8], [9] et [14].

On notera qu’un même échangeur peut assurer plusieurs fonctions dans des domaines applicatifs variés.

2. Technologiques des échangeurs

Il nous est difficile d’être exhaustif sur la description technologique des échangeurs tant la diversité de ces appareils et de leurs variantes en fonction des constructeurs est importante. La figure suivante rappelle de façon synthétique les principales classes d’échangeurs suivant des critères strictement technologiques :

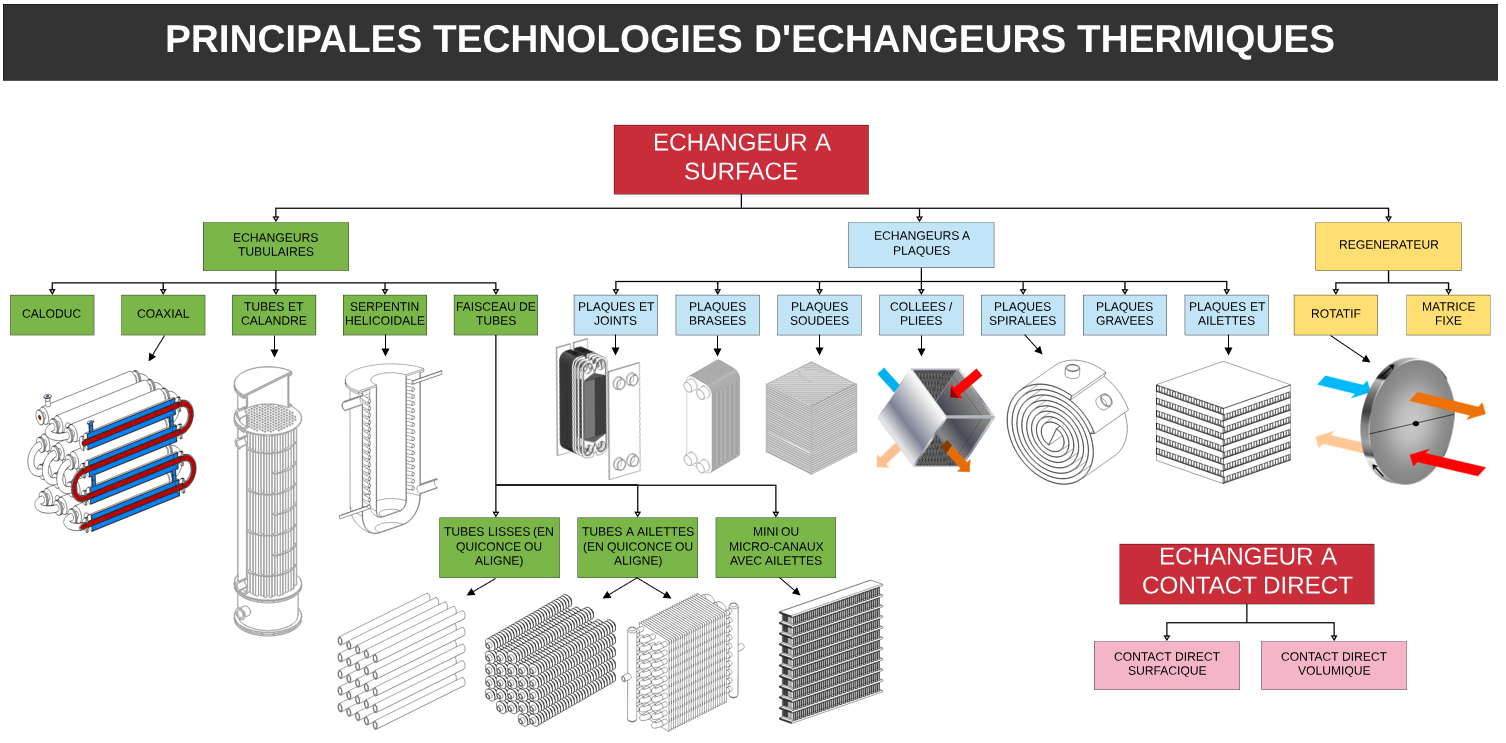Classification des échangeurs thermiques (à surface) en fonction de la technologie de fabrication [1]

 

Les échangeurs tubulaires (Tubes et calandre, coaxial…) sont les plus répandus et représentaient, en 1998, quasiment 50% des parts de marché en Europe. Les échangeurs dits compacts (échangeurs à plaques et joints par exemple), qui ont connus une croissance importante dans les années 90, tendent à faire diminuer ce pourcentage mais la grande adaptabilité des échangeurs tubulaires (tenue en pression et en température, diversité des matériaux…etc.) fait qu’il est difficile d’assurer leurs remplacements par d’autres technologies :

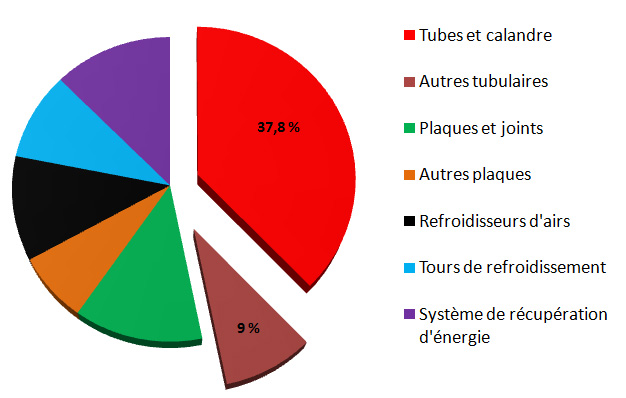Répartition en pourcentage des recettes par type d’échangeur sur le marché totale de l’échangeur en Europe (données 1998) [15]

3. Fonctionnement général d’un échangeur thermique

Il existe de nombreuses technologies d’échangeurs de chaleur, mais ils fonctionnent tous suivant les mêmes processus physiques d’échanges, c'est-à-dire :

• La conduction : Qui représente les échanges à travers les parois (le plus souvent métalliques),
• La convection : Qui représente les échanges entre les fluides et les parois,
• Le rayonnement : Qui représente les échanges radiatifs entre les fluides et les parois (principalement infra rouge) bien que ce dernier soit souvent négligeable (car pris en compte uniquement pour un fonctionnement à haute température).

On distingue également trois modes d’écoulement différents :

- celui à co-courants (écoulements parallèles des fluides et dans la même direction)
- celui à contre-courants (écoulements parallèles des fluides mais dans des directions inverses)
- et celui à courants croisés (écoulements perpendiculaires entre les deux fluides)

Le mode de circulation influe également sur la qualité et l’efficacité du transfert : Un échangeur dit anti-méthodique (ou à co-courants) signifie que l’entrée des deux fluides (chaud et froid) se situe du même coté de l’échangeur. La configuration dite méthodique est celle ou les fluides circulent à contre-courants. On l’appelle méthodique car c’est cette configuration qui permet d’obtenir les meilleures performances d’échangeurs. En effet, pour une circulation à co-courant des fluides, la température de sortie du fluide chaud ne pourra pas être plus basse que la température de sortie du fluide froid tandis qu’à contre courant, il est possible d’abaisser la température du fluide chaud à une valeur qui tendra vers la température d’entrée du fluide froid. Nous verrons plus bas des représentations graphiques qui illustreront ces propos.

3.1 Calcul de la puissance thermique d’un échangeur : Le bilan thermique

L’équation de bilan d’énergie exprime, conformément au premier principe de la thermodynamique, l’égalité des flux de chaleur échangés par chacun des fluides circulant dans l’échangeur thermique, en négligeant les pertes vers l’extérieur [1].

La puissance échangée entre les deux fluides, dépend essentiellement de l’écart de température que celui-ci subit lorsque que l’échange se réalise par chaleur sensible, ou alors essentiellement de la valeur de la chaleur latente (correspondant à l’enthalpie de changement d’état) lorsqu’il y a un changement de phase (fluide diphasique).

3.1.1 Echange monophasique

Lorsque l’on parle de transfert monophasique, cela signifie que les fluides en présence restent sous une même et unique phase et ne changent pas d’état (il reste uniquement à l’état gazeux ou liquide) : les échanges de chaleur se traduisent ainsi uniquement par une élévation ou une baisse de leur température. On parle alors d’échange sous forme de chaleur sensible.

La puissance échangée (P en Watt) entre deux fluides à l’état monophasique, dépend essentiellement des trois critères suivants : Le débit massique des fluides (qm en [kg/s]), Les propriétés thermophysiques des fluides (masse volumique (ρ en [kg/m3]) et chaleur spécifique (Cp en [J/kg-K])), L’écart de température que vont subir les fluides (∆T en [K] ou en [°C]). La manière la plus simple de représenter un échangeur est la suivante (configuration co-courant).

Représentation soimplifiée d’un échangeur de chaleur

La chaleur se dirigeant toujours du fluide chaud vers le fluide froid et en faisant l’hypothèse que les échanges vers l’extérieur sont nuls (cas d’un échangeur isolé), on a logiquement :

$$\mbox{T entree chaud} > \mbox{T sortie chaud}$$
$$\mbox{T entree froid} < \mbox{T sortie froid}$$

De ce fait, on peut exprimer la puissance échangée par chacun des fluides avec les expressions suivantes qui impliquent la notion de conservation de l’énergie :

$$P=qm_c \times C p_c \times \Delta T_c = - q m_f \times C p_f \times \Delta T_f$$

Avec :
$$\Delta T_c = T_{e_c} - T_{s_c}$$
$$\Delta T_f = T_{e_f} - T_{s_f}$$

NB : On notera également que de manière générale, les valeurs des propriétés thermophysiques des fluides sont retenues comme étant des constantes calculées à la valeur moyenne de température et de pression de chacun des fluides.

Grâce à l’écriture de ces bilans thermiques, on peut ainsi facilement retrouver une grandeur (par exemple la température de sortie du fluide froid) si on connait l’ensemble des autres grandeurs.

Une représentation assez courante des échanges thermiques entre deux fluides est le diagramme Température-Enthalpie (ou Température-Puissance). Dans le cadre d’un échange par chaleur sensible uniquement, la représentation est la suivante :

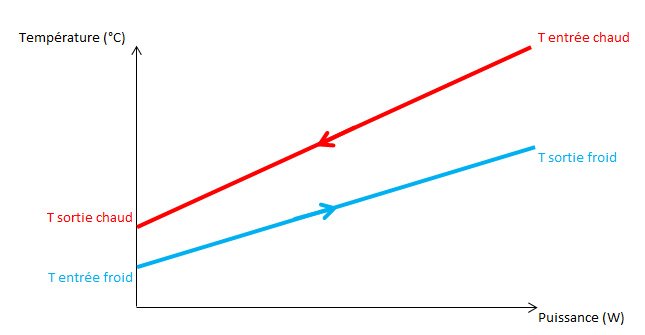Représentation du diagramme Température-Puissance pour des échanges monophasique/monophasique

Ici, on illustre une configuration à contre courant (comme pour les exemples qui suivent) où le fluide chaud (en rouge) entre du coté opposé à celui du fluide froid (en bleu) : On rappel que dans cette configuration, le fluide chaud peut être refroidit à un niveau plus bas que la température de sortie du fluide froid tandis que le fluide froid peut, lui aussi, être chauffé à une température plus haute que la température de sortie du fluide chaud.

3.1.2 Echange diphasique

Lorsque l’on parle de transfert diphasique, cela signifie que les fluides en présence vont changer d’état (ou de phase) entre l’entrée et la sortie de l’échangeur : les échanges de chaleur se traduisent ainsi quasiment uniquement par un changement d’état sans élévation ni baisse de leur température (pour les corps pures à pression constante). On parle alors d’échange sous forme de chaleur latente.

Les changements de phase les plus fréquemment rencontrés dans le domaine des échangeurs de chaleur sont l’évaporation (Liquide → Gaz) et la condensation (Gaz → liquide), notamment dans le domaine du génie climatique (cycle des pompes à chaleur pour la production de froid) et de la production d’énergie électrique (via un cycle de Rankine pour la production d’énergie mécanique (puis électrique via un alternateur)…etc.).

Les autres changements de phase, tels que la fusion et la solidification, restent encore des domaines plus marginaux bien qu’appliqués de plus en plus par l’utilisation grandissante des MCP (Matériaux à Changement de Phase). On citera également la sublimation (solide→ Gaz) qui est utilisé, par exemple, dans les process de lyophilisation.

La puissance échangée (P en [W]) entre deux fluides qui vont changer de phase dépend essentiellement des trois critères suivants :

• Le débit massique des fluides (qm en [kg/s]),
• La chaleur latente ou enthalpie de changement de phase (liquide/vapeur le plus couramment) qui est une propriété thermophysique des fluides (noté Lv ou ∆hlv en [J/kg]),
• Le titre massique (noté xv) d’une des phases (en général la phase vapeur pour un mélange liquide/vapeur). Ce titre massique est définit comme le rapport du débit massique de la phase vapeur au débit massique des deux phases (c'est-à-dire le débit massique total de fluide), il est donc compris entre 0 (phase totalement liquide) et 1 (phase totalement vapeur) :

$$x_v=\frac{qm_v}{(qm_v+qm_l)}=\frac{qm_v}{qm_{total}}$$

Pour une évaporation (ou une condensation) totale, on peut donc dire que l’on passe d’un titre de vapeur de 0 à un titre de vapeur de 1 (ou inversement pour la condensation) donc ∆xv=1. Ainsi, l’expression de la puissance est la suivante :

$$P=qm_c \times \Delta h_{vl_c}=-qm_f \times \Delta h_{lv_f}$$

Dans le cadre de cette expression, le fluide chaud (indice c) va par exemple se condenser totalement et le fluide froid va s’évaporer totalement. On a ainsi les expressions suivantes pour le calcul de l’enthalpie de changement de phase :

$$\Delta h_{vl_c}=H_{v_c}-H_{l_c}$$
$$\Delta h_{lv_f}=H_{l_c}-H_{v_c}$$

NB : On notera que la détermination de l’enthalpie de changement de phase est dépendante de la pression ou de la température de saturation du fluide (en sachant que ces deux paramètres sont dépendants l’un de l’autre).

Lorsque la condensation ou l’évaporation est partielle (i.e. 0 < xv < 1), on fait alors intervenir la différence du titre massique entre l’entrée et la sortie du fluide : La puissance échangée s’exprime ainsi par :

$$P=qm_c \times \Delta h_{vl_c}\times \Delta x_v=-qm_f \times \Delta h_{lv_f} \times \Delta x_v$$

Pour un changement de phase sur le fluide froid (évaporation) avec un fluide chaud monophasique, on peut par exemple rencontrer l’évolution suivante dans le diagramme Température-Puissance :

Représentation du diagramme Température-Puissance pour un échange de type Evaporation / Monophasique

Ici, le fluide froid entre dans l’échangeur à l’état liquide saturé (par exemple eau liquide à 1 bar et 100°C donc xv=0) et s’évapore jusqu’à saturation vapeur (par exemple vapeur d’eau à 1 bar et 100°C donc xv=1) par l’apport d’énergie thermique issue du fluide chaud qui par conséquent se refroidit.

Pour un changement de phase sur le fluide chaud (condensation) avec un fluide froid monophasique, on peut avoir l’évolution du diagramme Température-Puissance qui suit :

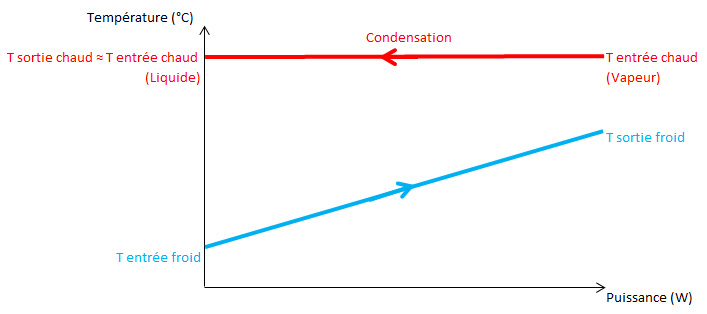Représentation du diagramme Température-Puissance pour un échange de type Condensation / Monophasique

Ici, nous somme dans la situation inverse : Le fluide chaud entre dans l’échangeur à l’état vapeur saturée et se condense jusqu’à saturation par l’extraction d’énergie thermique issue du réchauffement du fluide froid.

3.1.3 Echange monophasique et diphasique

Lors d’un échange par changement de phase, il est fort probable que les fluides disponibles ne soit pas exactement à l’état saturé (pour l’eau, l’état de saturation à la pression atmosphérique est atteint à environ 100°C). De ce fait, l’échangeur va devoir coupler les échanges monophasiques (sensibles) et diphasiques (changements de phase=latent). Pour le calcul de la puissance, on devra alors additionner les deux expressions vues plus amont pour calculer la puissance totale échangée.

Par exemple chauffer un fluide liquide jusqu’à saturation puis l’évaporer partiellement ou totalement (ou refroidir un fluide gazeux jusqu’à saturation pour le condenser partiellement ou totalement), dans ce mode de fonctionnement, on pourra donc additionner les deux expressions vues en amont pour calculer la puissance totale échangée :

$$P=qm_c\times Cp_c \times \Delta T_{c_{v_{sat}}}+qm_c \times \Delta h_{vl_c} \times \Delta x_{v_c} =qm_c \times (Cp_c \times \Delta T_{c_{v_{sat}}}+ \Delta h_{vl_c}\times \Delta x_{v_c})$$
$$-P=qm_f\times Cp_f \times \Delta T_{f_{l_{sat}}}+qm_f \times \Delta h_{lv_f} \times \Delta x_{v_f} =qm_f \times (Cp_f \times \Delta T_{f_{l_{sat}}}+ \Delta h_{lv_f}\times \Delta x_{v_f})$$

Enfin, il arrive fréquemment de devoir surchauffer de la vapeur à la suite de l’évaporation totale ou bien de sous refroidir un liquide à la suite d’une condensation totale. L’expression de la puissance devient alors la suivante :

$$P=qm_c\times Cp_{c_v} \times \Delta T_{c_{v_{sat}}}+qm_c \times \Delta h_{vl_c}+qm_c\times Cp_{c_l} \times \Delta T_{c_{l_{sat}}}$$
$$=qm_c \times ( Cp_{c_v} \times \Delta T_{c_{v_{sat}}}+ \Delta h_{vl_c}+Cp_{c_l} \times \Delta T_{c_{l_{sat}}})$$

$$-P=qm_f\times Cp_{f_l} \times \Delta T_{f_{l_{sat}}}+qm_f \times \Delta h_{lv_f}+qm_f\times Cp_{f_v} \times \Delta T_{f_{v_{sat}}}$$
$$=qm_f \times (Cp_{f_l} \times \Delta T_{f_{l_{sat}}}+\Delta h_{lv_f}+Cp_{f_v} \times \Delta T_{f_{v_{sat}}})$$

Avec :

$$\Delta T_{c_{v_{sat}}}=T{e_c}-T_{sat(x=1)_c}$$ $$\Delta T_{c_{l_{sat}}}=T_{sat(x=0)_c}-T{s_c}$$

$$\Delta T_{f_{v_{sat}}}=T{s_f}-T_{sat(x=1)_f}$$ $$\Delta T_{f_{l_{sat}}}=T_{sat(x=0)_f}-T{e_c}$$

Pour un corps pur, on souligne que :

$$T_{c_{l_{sat(x=1)}}}=T_{c_{v_{sat(x=0)}}}$$

$$T_{f_{l_{sat(x=1)}}}=T_{f_{v_{sat(x=0)}}}$$

Pour un fluide chauffé, puis évaporé puis surchauffé par un fluide chaud qui est refroidi, condensé puis sous refroidi, on peut avoir l’évolution du diagramme température-puissance qui suit :

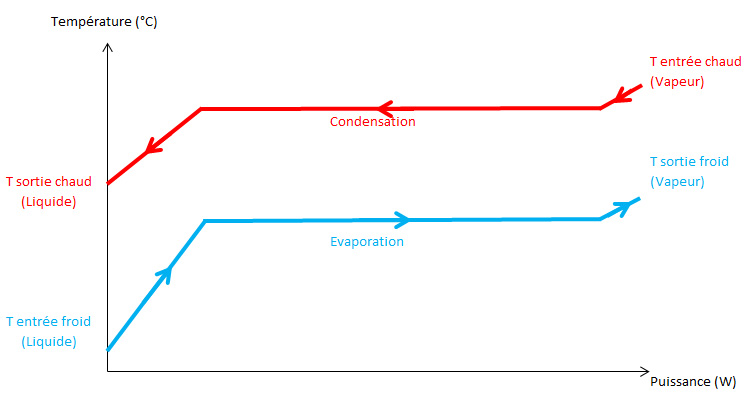Représentation du diagramme Température-Puissance pour un échange de type Evaporation / Condensation

Ici, l’énergie thermique permettant le chauffage, l’évaporation et la surchauffe du fluide froid est fournie par le refroidissement, la condensation ainsi que le sous-refroidissement du fluide chaud.

Nous avons vu l’expression de la puissance d’un échangeur par l’équation de la conservation de l’énergie à travers l’écriture des différentes expressions et en fonction des modes de transferts thermique (sensible, latent ou couplage sensible + latent). Nous n’avons cependant pas abordé le fond du problème du dimensionnement de l’échangeur. En effet, ces premiers calculs permettent de connaitre les principales grandeurs (puissance, débit, température) qui vont conditionner le dimensionnement, c'est-à-dire les dimensions (la taille), de l’échangeur.

Pour cela, nous allons introduire les deux principales méthodes de dimensionnement qui nécessite toutes deux le calcul du coefficient d’échange thermique global.

3.2 Méthodes de dimensionnement

Au côté de l’équation de bilan d’énergie, la résolution des problèmes d’échange thermique nécessite l’écriture d’une seconde équation, de nature tout à fait différente de la première, qui pour rappel est une équation thermodynamique et traduit le principe de conservation de l’énergie. Cette seconde équation est l’équation de transfert de chaleur qui traduit la relation entre le flux de chaleur échangé et la différence de températures disponibles entre les deux fluides qui circulent dans l’échangeur thermique.

Le dimensionnement d’un échangeur consiste à calculer la surface d’échange nécessaire pour obtenir les performances désirées (puissance, température de sortie). Il faudra par la suite déterminer les pertes de charge (pertes de pression) que va engendrer la circulation des fluides (par la friction contre les parois du fait de la viscosité) afin de vérifier la concordance avec le cahier des charges (qui impose souvent une limite haute en terme de valeur d’une perte de charge. Cette valeur haute correspondant, la plupart du temps, à une capacité de pompage existante et donc à ne pas dépasser).

NB : Pour la détermination des pertes de charge par le calcul du facteur de friction, le lecteur pourra se reporter aux ouvrages [1], [2], [5], [6] et surtout à [16] qui constitue l’ouvrage de référence.

Pour connaitre la surface d’échange de l’échangeur, il faut dans un premier temps connaitre les grandeurs dimensionnantes telles que la puissance, les températures, les débits : Nous avons vu plus haut comment déterminer ces grandeurs par les bilans thermiques.

Ensuite, il faut calculer, et ce quelque soit la méthode de dimensionnement utilisée, les coefficients d’échanges thermiques partiels et le coefficient d’échange thermique global.

3.2.1 Coefficient d’échange global et partiel

Pour expliquer clairement la notion de coefficient d’échange, on considère une paroi métallique au travers de laquelle la chaleur est transférée par conduction, cette paroi étant en contact avec un fluide chaud et sur son autre face avec un fluide froid : cette situation se traduit par un transfert de chaleur entre les deux fluides. On peut exprimer par l’équation qui suit la relation entre le flux de chaleur transféré P, l’écart de température ∆T des deux fluides (le chaud (indice c) et le froid (indice f)) et l’aire S de la paroi d’échange :

$$P=U\times S \times (T_c-T_f) = \frac{(T_c-T_f)}{R_{global}}$$

Cette équation plus connue sous le nom de loi de Newton caractérise le transfert de chaleur entre les deux fluides et introduit ainsi de nouvelles grandeurs :

• le facteur U dont l’unité est en [W/m²-K] qui exprime la qualité du transfert de chaleur entre les deux fluides s’écoulant de part et d’autre de la paroi. Ce facteur est désigné comme le coefficient d’échange thermique global entre les deux fluides (CETG) ;
• le facteur Rg, inverse du produit U.A, dont l’unité est en [K/W] appelé résistance thermique globale (RTG) dont le concept est issu directement de l’analogie avec la résistance électrique de la loi d’Ohm dans le domaine du génie électrique. Cette analogie associe la différence de température à la différence de potentiel et le flux de chaleur à l’intensité électrique. La loi de Newton est alors analogue à la loi d’Ohm.

Comme nous l’avons dit, une grande part du calcul d’un échangeur repose sur l’évaluation de ce coefficient d’échange global dont la valeur peut être très différente suivant le type de paroi en contact avec les fluides, les fluides et leurs propriétés, l’état du fluide (simple phase gazeux ou liquide, double phase), les modes de transfert entre les fluides et la paroi (réchauffement ou refroidissement, évaporation, condensation…). Bien que le calcul d’un échangeur nécessite l’évaluation précise du coefficient d’échange global, il est indispensable de connaître les ordres de grandeur des coefficients d’échanges globaux dans diverses conditions, notamment pour juger rapidement de la justesse d’un calcul :

Situation physique	U en W/m²-K
condenseur de vapeur d’eau	1100-1600
réchauffeur d’eau	1100-5600
condenseur de fluide frigorigène de type HFC avec eau comme fluide secondaire	500-1000
échangeur eau-eau	850-1800
batteries à ailettes (tube : eau, ailette : air)	25-70
échangeur eau/huile	110-350
condenseur d’ammoniac avec eau comme fluide secondaire	850-1400
échangeur gaz/gaz	10-40
évaporateur de HFC à tubes et calandre à détente directe	800-1600
Evaporateur noyé de HFC à tubes et calandre	500-1200

Ordre de grandeur du coefficient d’échange global [1]

On notera que la valeur de ce coefficient est avant tout gouvernée par la résistance thermique convective (c’est à dire le transfert entre la paroi et le fluide), la résistance par conduction étant très faible dans la majorité des cas (car les parois sont de faible épaisseur et de conductivité thermique élevée). Ce point souligne alors l’importance d’une bonne évaluation des transferts thermiques par convection.

Le coefficient d’échange global U se calcul à partir des différentes résistances thermiques de convection (interne et externe), de conduction (paroi solide) et éventuellement des résistances d’encrassement (dépôt biologique, tartre...etc.) :

1 - La résistance de conduction due à la présence d’une paroi solide s’exprime grâce à l’équation de la chaleur, elle est fonction de la géométrie de la paroi (coordonnées plan, cylindrique ou sphérique). Elle dépend aussi de la nature du matériau (conductivité thermique).

Si la conduction est monodirectionnelle comme cela est le cas dans une paroi plane, on utilise l’expression suivante :

$$R_{conduction}=\frac{e}{\lambda \times S}$$

Si la conduction est réalisée dans une paroi cylindrique, on utilise l’expression qui suit :

$$R_{conduction}=\frac{1}{2\pi \times \lambda \times L} \times \ln \left(\frac{D_{ext}}{D_{int}}\right)$$

2 - Les résistances thermiques de convection sont en fait l’inverse du coefficient d’échange convectif h (interne et externe). Chaque coefficient d’échange convectif est calculé à partir de la valeur du nombre adimensionnel de Nusselt qui est évalué par des corrélations empiriques (par expérimentation) données en fonction de la géométrie (diamètre par exemple), des régimes d’écoulement (laminaire, transitoire ou turbulent) et de nombres adimensionnels (Reynolds (Re), Prandtl (Pr)). De manière générale, les expressions du nombre de Nusselt (Nu) apparaissent sous la forme suivante :

$$N u=h\times \frac{D_h}{\lambda}=A\times R e^x \times P r^y$$

Ces corrélations sont spécifiques aux produits de beaucoup de constructeur et possèdent des domaines de validité bien précis (géométrie, intervalle de la valeur du nombre de Reynolds et du nombre de Prandtl) qu’il est impératif de respecter pour minimiser les erreurs sur ces données. On trouve ces corrélations dans différents ouvrages ([2], [5], [6]), notamment au GRETh (référence [2]) où une revue exhaustive des méthodes existantes est disponible.

A titre d’exemple, la plus courante de ces expressions – appelée corrélation de Colburn (Nom de l’auteur) - permet de déterminer le coefficient d’échange convectif d’un fluide s’écoulant dans une section circulaire (tube) en régime turbulent (régime d’écoulement le plus favorable aux échanges thermiques convectifs et intervenant pour un nombre de Reynolds > 10 000 dans un tube de section circulaire) :

$$N u=0.023\times R e^{0.8} \times P r^{1/3}$$

Comme $$N u=h\times \frac{D_h}{\lambda}$$

On peut alors déterminer le coefficient d’échange convectif partiel h :
$$h=\frac{\lambda}{D_h}\times 0.023\times R e^{0.8} \times P r^{1/3}$$

La résistance thermique convective s’exprime alors par :
$$R_{convection}=\frac{1}{h \times S}$$

3 - Enfin, les valeurs des résistances d’encrassement. En général, l’encrassement des échangeurs de chaleur est défini comme le dépôt de matériaux ou de substances non désirées sur les surfaces d’échanges. Ce dépôt peut être constitué de cristaux, de sédiments, de résidus biologiques, de produits d’une réaction chimique ou bien encore être la combinaison de plusieurs de ces éléments. C’est un processus qui est dynamique et qui se déroule de façon continue ou ponctuelle, généralement jusqu’à atteindre un état d’équilibre (valeur asymptotique) ou jusqu’à ce qu’il soit nécessaire de nettoyer l’échangeur – la période d’encrassement pouvant varier de quelques heures à plusieurs mois, voire plusieurs années. Ces résistances thermiques d’encrassement sont en général données par les standards TEMA (Tubular Exchanger Manufacturer Association [7]) qui font office de référence (sauf retour d’expérience propre à l’exploitant). Leur prise en compte dans le calcul du coefficient d’échange global permet de simuler le fonctionnement de l’échangeur en conditions dégradées (avec une résistance d’encrassement suite à un nombre d’heures de fonctionnement) et permet de faire un surdimensionnement « justifié » due à une potentielle future baisse de performance. En effet, l’ajout d’une ou plusieurs résistances d’encrassement a pour effet néfaste de dégrader la valeur du coefficient d’échange thermique global, induisant une hausse de la surface d’échange nécessaire et donc un surplus en cout matière et conception.

Pour plus d’informations sur l’encrassement, vous pouvez vous référer à [1], [3] ainsi qu’à [12] et [13] qui traitent le sujet de manière assez exhaustive.

Schématisation des différentes résistances thermiques d’une paroi [1]

La résistance globale (et en conséquence U) se déduit de la règle d’additivité des résistances partielles :
$$R_{global}= \frac{1}{U \times S} = \sum R_i$$

On notera que le coefficient d’échange global doit être défini par rapport à une surface d’échange de référence. Dans le cas, d’une paroi plane, cette surface de référence est évidente puisqu’unique : c’est la surface de la paroi. Dans le cas d’une paroi tubulaire (cylindrique), deux surfaces d’échange de référence peuvent être retenues : la paroi interne ou externe. On peut alors choisir indistinctement l’une ou l’autre à la condition de maintenir, tout au long du calcul ce choix.

Ainsi, le coefficient d’échange global U (défini par rapport à la surface d’échange interne – notée avec un indice int - pour les échangeurs tubulaires) est déterminé par la relation suivante dans laquelle interviennent la résistance de paroi, les résistances convectives et les résistances d’encrassement :

$$R_{global}= R_{convection_{ext}}+R_{encrassement_{ext}}+R_{conduction}+R_{encrassement_{int}}+R_{convection_{int}}$$

Cette expression prend différentes formes suivant le type d’échangeur considéré (en négligeant les résistances d’encrassement) :

• Pour un échangeur tubulaire (de diamètre externe Dext et interne Dint) :
  $$\frac{1}{U_{int}\times S_{int}}=\frac{1}{h_{ext}\times S_{ext}}+\frac{1}{2\pi \times \lambda \times L}\times \ln \left(\frac{D_{ext}}{D_{int}} \right)+\frac{1}{h_{int}\times S_{int}}$$
  En sachant que : $$S_{int}=\pi \times D_{int} \times L$$
  On a finalement : $$\frac{1}{U_{int}}=\frac{1}{h_{ext}}\times \left(\frac{S_{int}}{S_{ext}}\right)+\frac{D_{int}}{2\lambda} \ln \left(\frac{D_{ext}}{D_{int}} \right) + \frac{1}{h_{int}}$$
• Pour un échangeur à plaques (d’épaisseur e) :
  $$\frac{1}{U}=\frac{1}{h_{c}}+\frac{e}{\lambda} + \frac{1}{h_{f}}$$

3.2.2 Méthode de l’écart de température moyen logarithmique

La représentation des évolutions de températures moyennes des fluides en fonction d’une grandeur spatiale (par exemple, x, la distance d’un des fluides par rapport à l’entrée de l’échangeur) suppose la résolution simultanée des deux équations :

• équation de bilan énergétique ;
• équation de transfert de chaleur.

L’écriture des équations d’énergie et de transfert, pour un échangeur à co-courant sur un élément de surface dS, est la suivante :

$$\mbox{d}P=qm_c \times C p_c \times \mbox{d} T_c = - q m_f \times C p_f \times \mbox{d} T_f$$
$$\mbox{d}P=U\times \mbox{d} S \times \Delta T$$

A partir de ces deux équations, nous déduisons l’équation différentielle :
$$\mbox{d}(\Delta T)=\mbox{d}T_c-\mbox{d} T_c = -\mbox{d}P \times \left(\frac{1}{qm_c \times C p_c }+\frac{1}{ q m_f \times C p_f}\right) \times \mbox{d} S$$

D'où :
$$\frac{\mbox{d}(\Delta T)}{\Delta T}=-U \times \left(\frac{1}{qm_c \times C p_c }+\frac{1}{ q m_f \times C p_f}\right) \times \mbox{d} S$$

L’intégration de cette dernière équation donne l’évolution spatiale de l’écart de température entre les fluides à partir de celui existant entre les fluides à l’entrée de l’échangeur (x=0) en supposant constant le coefficient d’échange U et les capacités thermiques Cp :

$$\Delta T(x)=\Delta T(x=0) \times \exp \left(-U \times S \times \frac{x}{L} \times \left(\frac{1}{qm_c \times C p_c }+\frac{1}{ q m_f \times C p_f}\right) \right)$$

Pour un échangeur à contre-courant, l’expression précédente devient :
$$\Delta T(x)=\Delta T(x=0) \times \exp \left(-U \times S \times \frac{x}{L} \times \left(\frac{1}{qm_c \times C p_c }-\frac{1}{ q m_f \times C p_f}\right) \right)$$

Cette méthode est la seule méthode analytique permettant une représentation spatiale exacte de la température moyenne des fluides. On aura noté toutefois qu’elle suppose des hypothèses fortes telles que, entre autres, la constance du CETG tout le long de l’échangeur.

Les équations précédentes aboutissent, après intégration aux bornes de l’échangeur, à l’expression suivante qui relie la puissance échangée, le coefficient d’échange global et la surface d’échange totale :

$$P=U\times S\times \frac{\Delta T_a - \Delta T_b}{\ln \left(\frac{\Delta T_a}{\Delta T_b}\right)}=U\times S \times \Delta T_{ln}$$

La différence de température moyenne logarithmique ΔTln est définie de la manière suivante :
$$\Delta T_{ln}=\frac{\Delta T_a - \Delta T_b}{\ln \left(\frac{\Delta T_a}{\Delta T_b}\right)}$$

Cette expression fait intervenir les paramètres ∆Ta et ∆Tb qui représentent les écarts de températures aux deux bornes de l’échangeur. Elle s’applique aussi bien aux échangeurs à co-courants qu’à contre-courants :

Représentation de ΔTa et ΔTb en fonction de la configuration d’écoulement

Dans le cas où la condition de courant parallèle des fluides n’est pas respectée, c'est-à-dire pour une configuration à courant croisés (comme c’est le cas pour des batteries à ailettes), un aménagement de la méthode est réalisé en introduisant un facteur correctif F qui prend en compte la spécificité de l’échangeur. Ainsi, la différence de température moyenne logarithmique correspond à la valeur en contre-courants multipliée par le facteur de correction F (répertorié dans des abaques spécifiques aux configurations à courants croisés possible (1 fluide brassé, 2 fluides brassés...etc.)). Ce facteur F à donc une valeur comprise entre 0 et 1.

La méthode de dimensionnement par l’écart de température logarithmique se résume donc à une succession d’opérations simples dont l’organigramme suivant synthétise les principales étapes :

Démarche de dimensionnement par la méthode du ∆Tln [1]

Cette méthode permet essentiellement la détermination de la surface S de l’échangeur et ne s’applique que dans des conditions strictes [1] :

• le coefficient d’échange global est supposé constant,
• les échangeurs sont à circulation parallèle (co ou contre-courant) ou corrigé d’un facteur F si ce n’est pas le cas,
• les capacités thermiques massiques des fluides sont supposées constantes tout au long du processus.

La méthode de l'écart logarithmique, si elle est commode pour évaluer une surface d'échange (les quatre températures des fluides étant connues a priori) présente une limite d’utilisation lorsqu'il s'agit d'évaluer la puissance thermique échangée pour un échangeur de surface connue. Une méthode - celle de l'efficacité et du Nombre d'Unités de Transfert (NUT) - est proposée pour éviter cette difficulté. L’objet de cette dernière méthode de dimensionnement est d’évaluer la puissance thermique transférée dans un échangeur dont la géométrie est connue.

3.2.3 Méthode de l’efficacité et du nombre d’unité de transfert

On définira l'efficacité ɛ d'un échangeur comme le rapport du flux de chaleur réellement échangé dans l’échangeur (d’arrangement géométrique quelconque) au flux de chaleur maximum qu'il est possible d'échanger (c’est à dire le flux échangé avec une surface d’échange infinie…) pour un échangeur à circulation à contre-courant fonctionnant avec des débits et des températures d’entrée des fluides identiques à ceux du cas considéré.

Le flux de chaleur maximum qu'il est possible d'échanger est déterminé de la façon suivante: la variation de température maximale que peut subir le fluide de plus faible débit de capacité thermique (Le débit de capacité thermique noté (C ) ̇et exprimé en [W/K] est le produit du débit massique (qm) par la chaleur spécifique (Cp)) est égale la différence entre les températures d'entrée des fluides.

Le fluide qui est susceptible de subir cette variation maximale est le fluide qui présente le débit de capacité thermique massique minimale :
$$\dot{C}_{min}=\min (qm_c \times Cp_c ;qm_f×Cp_f )=\min (\dot{C}_c;\dot{C}_f)$$

Ce résultat serait obtenu avec une surface d'échange infinie et un échangeur à contre-courant.

Le flux de chaleur maximum possible est donc:

$$P_{max}=\dot{C}_{min}\times (T_{e_c}-T_{e_f})$$

L'efficacité de l’échangeur thermique peut alors s'écrire :

• si le coté chaud présente le produit qm*Cp minimum :
  $$\epsilon = \frac{P_{reel}}{P_{max}}=\frac{\dot{C}_{c}\times (T_{e_c}-T_{s_c})}{\dot{C}_{c}\times (T_{e_c}-T_{e_f})}=\frac{ (T_{e_c}-T_{s_c})}{ (T_{e_c}-T_{e_f})}=\frac{\Delta T_c}{\Delta T_{max}}$$
• si le coté froid présente le produit qm*Cp minimum :
  $$\epsilon = \frac{P_{reel}}{P_{max}}=\frac{\dot{C}_{f}\times (T_{s_f}-T_{e_f})}{\dot{C}_{f}\times (T_{e_c}-T_{e_f})}=\frac{ (T_{s_f}-T_{e_f})}{ (T_{e_c}-T_{e_f})}=\frac{\Delta T_f}{\Delta T_{max}}$$

Ainsi, d’une manière générale, l'efficacité est égale à la variation de température sur le fluide de (C ) ̇minimum sur l’écart de température maximale dans l'échangeur.

Lorsque l’on ne connait pas les températures de sortie (ce qui est souvent le cas dans le cadre d’une simulation), l’efficacité d’un échangeur ɛ est déterminée par le coefficient d’échange global U, la surface d’échange S et la valeur du paramètre $$\dot{C}_{min}$$ et $$\dot{C}_{max}$$ via l’introduction du terme de rapport de débit de capacité thermique noté $$C=\frac{\dot{C}_{min}}{\dot{C}_{max}}$$.

Les expressions qui relient ces grandeurs se déduisent de l’intégration des équations de bilan et de transfert.

Ainsi, on peut déduire,

• pour une circulation des fluides à contre-courants :
  $$\epsilon = 1- \frac{\exp (-NUT \times (1+C))}{1+C}$$
• pour une circulation des fluides à co-courants :
  $$\epsilon = \frac{1-\exp (-NUT \times (1+C))}{1-C \times \exp (-NUT \times (1+C))}$$

Le rapport $$U \times \frac{S}{\dot{C}_{min}}$$ est désigné comme le NUT (Nombre d'Unités de Transfert). Cette grandeur est égale, si l’on applique les équations de bilan et de transfert à :
$$NUT = U \times \frac{S}{\dot{C}_{min}} = \frac{P}{\Delta T_{ln}} \times \frac{T_{e_{(C_{min})}} -T_{s_{(C_{min})}}}{P}= \frac{T_{e_{(C_{min})}} -T_{s_{(C_{min})}}}{\Delta T_{ln}}$$

Soit le rapport de la variation de température sur le fluide de $$\dot{C}$$ le plus faible, à l’écart de température logarithmique.

La méthode dite de l’efficacité et du NUT (méthode ɛ-NUT) est une méthode aisée de calcul des performances d’un échangeur thermique (diagnostic). En effet la formulation proposée permet à partir du coefficient d'échange global U, la surface d’échange S, des débits massiques et chaleurs spécifiques :

• en premier lieu d'évaluer le nombre d’unités de transfert NUT ;
• en deuxième lieu, à partir des expressions précédentes ou de celles issues d’abaques pour des configurations plus complexes d’échangeurs, de calculer l’efficacité de l’échangeur ;
• l’efficacité connue, il est aisé de déterminer la température de sortie de l'un des fluides (celui présentant le C ̇ minimum). Ensuite, la température de sortie de l'autre fluide se déduit des bilans thermiques.

Les limitations de cette méthode sont identiques à celles de la méthode de l'écart de température moyen logarithmique. La mise en œuvre de cette méthode nécessite la connaissance de la relation entre l'efficacité et le Nombre d'Unités de Transfert. Cette relation sous forme d'abaque ou d'expressions algébriques dépend :

• du mode de circulation des fluides,
• du type d'échangeur de chaleur,
• du mélange ou non des filets fluides lorsque l’écoulement est à courant-croisé.

Remarque : Dans le cas de condenseur ou d’évaporateur (avec température constante du fluide à 2 phases), on considère Cmax tend vers une valeur infinie car la température de changement de phase est constante correspondant au fluide frigorigène qui s’évapore ou se condense.

3.3 Remarques sur les méthodes de calcul des échangeurs de chaleur

Pour le dimensionnement (méthode du ∆Tln) comme pour la simulation (méthode ɛ-NUT) du fonctionnement d’un échangeur, trois situations types peuvent être rencontrées :

1. Dans l’échangeur circulent des fluides présentant des propriétés thermophysiques constantes et le coefficient d’échange admet une valeur sensiblement constante : la méthode de calcul dite « point » consiste à appliquer sur l’ensemble de l’échangeur l’une des méthodes présentée.

2. Dans l’échangeur circulent des fluides dont l’un au moins présente une variation brutale de ses propriétés : cas d’un fluide liquide qui devient vapeur puis d’une vapeur surchauffée, par exemple. On ne peut légitimement pas accepter l’hypothèse de constance des propriétés et du coefficient U. La méthode « par zones » qui consiste à découper virtuellement l’échangeur en un nombre limité de zones (2 voire 3) caractérisées par la constance (ou quasi constance) des propriétés et de U dans chaque zone, permet d’utiliser les méthodes classiques précédentes pour chacune d’elles.

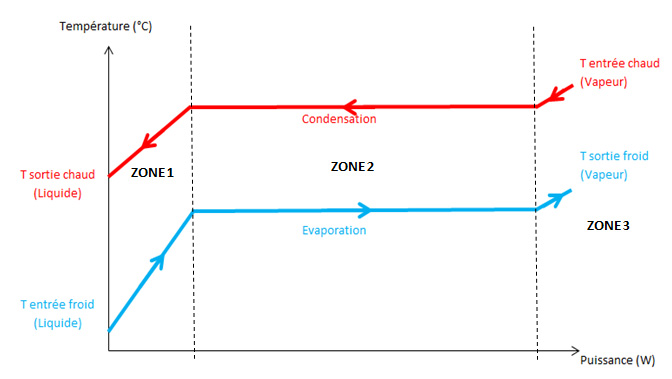Représentation du découpage par zone pour le dimensionnement dans un diagramme Température-Puissance pour un échange de type Evaporation / Condensation

3. Dans l’échangeur circulent des fluides dont les propriétés, le coefficient U varient continument de façon importante (par exemple pour un fluide à l’état supercritique très proche du point critique) : les méthodes précédentes ne peuvent plus s’appliquer. Les méthodes numériques à éléments ou volumes finis doivent s’appliquer en considérant l’échangeur comme une succession de mailles élémentaires pour lesquelles on établit les équations de bilan thermique, les équations locales de transfert de chaleur et les évaluations de pertes de pression.

Ces méthodes de complexité croissante sont toutes utilisées. La dernière méthode (par éléments ou volumes finis), de par sa complexité et la lourdeur des calculs qu’elle implique, nécessite des outils numériques lourds (voir $7).

4. Critères de performance d’un échangeur

Il existe plusieurs critères de performance d’un échangeur :

• L’efficacité d’un échangeur est un critère de performance important.
• Le coefficient d’échange global U (ou K) est aussi un des plus utilisé. Plus ce dernier est important, plus l’échangeur est performant. Il faut néanmoins que les pertes de charge soient les plus faibles possibles (mais suffisante afin d’assurer une bonne distribution des fluides) mais sont totalement dépendantes du design de l’échangeur.
• Enfin, le critère de compacité est aussi important car il est défini par le rapport de l’aire de la surface d’échange au volume de l’échangeur. R.K. Shah [4] propose qu’un échangeur soit considéré comme compact si sa compacité (rapport de la surface d’échange sur le volume de l’échangeur) est supérieure à 700 m²/m3 ; cette valeur est susceptible de varier de 500 à 800 m²/m3.

5. Le choix technologique : Identification des caractéristiques d’usages nécessaires à une sélection adaptée d’un échangeur thermique [1]

La sélection d’une technologie est une phase essentielle dans le projet d’un système ou d’un équipement thermique. Les critères techniques et économiques sont nombreux alors que le choix des technologies d’échangeurs thermiques est extrêmement varié.

La démarche entreprise pour aider le lecteur à assurer une sélection raisonnée est :

• d’identifier l’ensemble des critères techniques de choix ;
• de quantifier dans la mesure du possible des critères « qualitatifs » tels que les caractéristiques encrassantes d’un fluide, les risques associés à des défauts d’étanchéité…

Nous allons énumérer les différentes caractéristiques qui sont nécessaires pour amorcer les étapes de choix technologique d’un échangeur thermique. Ces grandeurs sont en premier lieu les données du procédé dans lequel l’échangeur doit être intégré, puis des caractéristiques associées aux contraintes spécifiques.

- Les fluides de transfert, moteur et frigorigène du procédé

En premier lieu, il faut pouvoir définir le plus précisément possible les différentes données du process dans lequel l’échangeur est prévu d’être intégré. Cela passe inévitablement par la définition des fluides utilisés et de leurs conditions d’usage. La définition des fluides du procédé est bien évidemment d’une importance capitale car il permet de définir les différentes propriétés thermophysiques des fluides qui seront mis en jeu et qui servent aux calculs des différentes grandeurs dimensionnelles et adimensionnelles.

- L’état des fluides de transfert (monophasique, diphasique)

- Les conditions extrêmes d’usage de l’échangeur

- Les températures maximales d’usage de l’échangeur
- La pression maximale de service de l’échangeur sur l’un ou l’autre des circuits
- Critère de pertes de charge maximales acceptables (ou de la perte de charge maximale…)

- L’encrassement des échangeurs thermiques

Ce critère demande une connaissance du potentiel encrassant du fluide qui peut induire plusieurs effets (Bouchage, Colmatage) et qui se traduisent par des effets sur la performance globale (Dégradation des performances thermiques, Augmentation des pertes de charge, Surdimensionnement). Ainsi, la question de l’encrassement est primordiale. Lors du fonctionnement avec des fluides à potentiel encrassant, il se peut qu’au bout d’un certain temps de fonctionnement de l’échangeur, celui-ci ne soit plus en mesure de fournir la puissance nécessaire. Il peut alors être judicieux d’écarter certaines typologies d’échangeurs qui sont très sensibles à ces phénomènes pour éviter, soit une dégradation trop importante et/ou rapide des performances de l’échangeur, soit pour préconiser une technologie d’échangeur qui permette une inspection et un nettoyage aisés pour assurer - et ceci tout au long de sa vie - les performances escomptées.

- Critère sur les exigences d’étanchéité de l’échangeur et les risques de fuite des fluides

La question des risques de fuite de fluides (et incidemment la qualité de l’étanchéité de l’échangeur) peut être un critère important notamment vis-à-vis de la sécurité de l’installation, les risques sur l’environnement. Ce critère peut être très contraignant en matière de choix technologique et peut intervenir dans le dimensionnement de l’échangeur lui-même par la nécessité d’une épaisseur de paroi importante (prenant en compte par exemple des scenarii de corrosion annuelle…), voir même des exigences de double paroi.

- Critère associé à la nécessité d’inspection des équipements techniques

Ce critère est d’une part attribué par des obligations d’ordre réglementaire de type DESP (Directive des Equipements Sous Pression) mais est aussi intimement lié aux critères précédents de l’encrassement et de l’étanchéité.

- Critère d’encombrement/compacité

La compacité d’un échangeur permet ainsi de juger rapidement de la performance d’un échangeur thermique. Ce critère peut aussi être déterminant en termes de choix technologique et de dimensionnement suivant la place (surface et/ou volume) que demande l’installation de l’échangeur dans le process.

- Critère de coût de l’échangeur

Ce critère reste le point sensible des relations fabricants / utilisateurs, surtout pour des applications bien connues, maitrisées et standardisées. Pour des applications plus spécifiques ou la réussite du projet est fortement conditionnée par la conception et la fabrication de l’échangeur, le critère du prix peut prendre moins d’importance.

6. Logiciels de dimensionnement des échangeurs de chaleur

Les problèmes de dimensionnement de ce composant primordial et essentiel concernent avant tout le traitement des aspects thermo-hydrauliques. La complexité du problème de calcul thermique des échangeurs vient de plusieurs facteurs et contraintes, notamment la diversité des technologies des appareils et la nature de la physique des écoulements. Il faut donc pour cela [3] :

• caractériser un modèle d’écoulement, surtout lorsque celui-ci est complexe ;
• choisir des corrélations empiriques adaptées : ce problème peut être précisément résolu par les fabricants en réalisant des campagnes d’essais qui permettent d’établir des corrélations propres à chacune de ses gammes d’échangeurs. Il est plus difficile pour les exploitants qui bénéficie de l’utilisation de technologie issue de plusieurs fabricants : dans ce cas, ils peuvent alors se rapporter aux corrélations qui sont présentées dans la littérature (voir [2], [5], [6]) ;
• adopter un algorithme de résolution : on peut en effet choisir des algorithmes de type dimensionnement ou de type simulation qui utilisent des méthodes analytiques ou numérique.

On fournit ci-dessous une liste non exhaustive des principaux logiciels de dimensionnement d’échangeur thermique :

• Xchanger suite de chez HTRI (Heat Transfer Research Incorporation) : Logiciel de référence qui inclut le dimensionnement des principales technologies d’échangeurs pour quasiment toutes les configurations standardisées (Tubes et calandre, plaques et joints, plaques et ailettes, batterie à ailette, Kettle …etc.) ;
• EDR (Exchanger Design and Rating) de chez AspenTech (anciennement HTFS) : Logiciel de référence qui inclut également le dimensionnement des principales technologies d’échangeurs pour quasiment toutes les configurations standardisées ;
• UNILAB, société italienne, développe depuis plus de 30 ans des logiciels pour l’énergie et notamment pour la sélection et le dimensionnement de composants, notamment les échangeurs de chaleur, associés au domaine du Froid et du Génie Climatique (Ventilo-convecteur, CTA, radiateur, batterie, stockage, échangeurs à tubes et calandre, micro-canaux…etc.) ;
• EchTherm de NeoTherm Consulting et diffusé exclusivement par le GRETh : Boîte à outils du thermicien qui inclut une multitude d’outils numériques permettant de dimensionner la majeure partie des technologies d'échangeurs thermiques (tubes et calandre, coaxial, échangeur à plaques, batterie à ailette, etc.) et pour quasiment tous les modes de transfert (monophasique, évaporateur, condenseur), d'aider au choix technologique, de faire des calculs experts de coefficient d'échange et de perte de charge. Il est également doté d'un panel d'outils dits "facilitateur du quotidien" pour, par exemple, faire des calculs de cycles (PAC, ORC), des calculs de propriétés thermo-physiques de fluides ou encore du calcul de réseaux d'échangeurs ;
• Les logiciels de CFD (Computational Fluid Dynamic) pour les méthodes par volumes ou éléments finis qui permettent la résolution couplée des équations de transferts thermiques et de la mécanique des fluides (Navier-Stockes). On citera les principaux logiciels comme Fluent de chez ANSYS, Comsol Multiphysics de chez COMSOL, SolidWorks Flow simulation de chez Dassault systèmes, STARCCM+ de CD-Adapco : Ces logiciels pointus sont réservés à la résolution de problèmes spécifiques liés au dimensionnement d’échangeur. Ils sont trop lourd (tarif et prise en main) pour la réalisation d’un dimensionnement simple mais souvent indispensable pour la recherche de nouvelles géométries complexes permettant d’améliorer les échanges thermiques, par exemple.
• Prosec de chez Prosim : Logiciels très puissants pour la simulation des échangeurs à plaques et ondes multifluides (applications cryogéniques (liquéfaction d’air) essentiellement) ;

Ce chapitre ne constitue pas une liste exhaustive de tous les logiciels disponibles sur le marché mais permet d’apprécier les principaux et surtout ceux qui sont utilisés par les industriels. On voit que le nombre de logiciels reste réduit et que l’utilisateur n’a que peu de choix sur les outils de dimensionnement d’échangeur. Certains développements ont permis de mettre en place des outils robustes, constamment mis à jour (cf. HTRI ; AspenTech) et qui sont parfois des outils imposés (code de calcul) dans certains Cahier Des Charges (CDC). Sans conteste, le développement d’un logiciel à usage interne reste marginal et réservé aux fabricants d’échangeurs thermiques.

7. Conclusions

Nous avons vu tout le long de cette notice que le dimensionnement d’un échangeur est un processus complexe et souvent sujet à de nombreuses contraintes et hypothèses. Il suppose en effet de préciser :

• la modélisation de l’échangeur retenu ;
• les propriétés thermophysiques des fluides ;
• le choix technologique réalisé ;
• les lois (corrélations) d’échange et de perte de pression spécifiques et adaptées ;
• les contraintes d’intégration et de design (compacité, performance thermique et perte de charge acceptable) ;
• les contraintes liées à l’utilisation de certains fluides (résistance d’encrassement, étanchéité, inspection);
• le choix d’un logiciel de calculs appropriés aux besoins ;
• le prix de l’échangeur (qui passe par sa conception, sa fabrication et sa mise en place).

A l’évidence le fait de disposer d’un échangeur bien adapté, bien dimensionné, bien réalisé et bien utilisé permet un gain non négligeable de rendement et donc d’énergie dans les process.

8. Notations et symboles

Symbole	Unité	Définition
A	-	Constante
C	-	Rapport des débits de capacités thermiques minimum sur maximum ($$C=\frac{\dot{C}_{min}}{\dot{C}_{max}}$$)
$$\dot{C}$$	W/K	Débit de capacité thermique ($$\dot{C}=qm. Cp$$
Cp	J/kg-K	Chaleur spécifique ou Chaleur massique ou Capacité thermique
D	m	Diamètre
Dh	m	Diamètre hydraulique ($$D_h=4.Sp/Pm$$(tube : Dh=D_int / espace annulaire Dh=Dext-Dint)
e	m	Epaisseur d’une paroi
h	W/m²-K	Coefficient d’échange convectif partiel (parfois noté α)
H	J/kg	Enthalpie massique
L	m	Longueur
Lv	J/kg	Chaleur latente (ou enthalpie de changement de phase liquide-vapeur)
Nu	-	Nombre de Nusselt
NUT	-	Nombre d’Unité de Transfert ($$NUT=U.S/C_{min}$$)
P	W	Puissance thermique
Pm	m	Périmètre mouillé
Pr	-	Nombre de Prandtl ($$Pr=\mu . C_p/\lambda$$
qm	kg/s	Débit massique
Re	-	Nombre de Reynolds ($$Re=\rho . V. D_h/\mu$$
R	K/W	Resistance thermique
S	m²	Surface d’échange
Sp	m²	Section de passage
T	K ou °C	Température
U	W/m²-K	Coefficient d’échange global (parfois noté K)
x	M	Longueur
xv	-	Titre massique rapporté à la phase vapeur

Lettre grecque

K ou °C

Symbole	Unité	Définition
ɛ	-	Efficacité thermique
λ	W/m-K	Conductivité thermique
µ	kg/m-s	Viscosité dynamique
ρ	kg/m3	Masse volumique
∆h	J/kg	Chaleur latente (ou enthalpie de changement de phase liquide-vapeur)
∆T	K ou °C	Différence de température
∆Tln	Ecart de température moyen logarithmique
∆xv	-	Différence du titre massique rapporté à la phase vapeur entre l’entrée et la sortie du fluide

Indice :

Symbole	Définition
c	chaud
e	entrée
ext	externe
f	froid
int	interne
l	liquide
min	minimum
max	maximum
s	sortie
sat	saturation (rapporté à l’état saturé d’un fluide)
v	vapeur

9. Références

[1] MARVILLET.C, MANIFICAT.A, BERRADA.N et WEBER.C ; E.Book TOME 1: Echangeurs Thermiques -: Technologies, Conception et dimensionnement, GRETh 2014.
[2] Manuel technique du GRETH, édition GRETh.
[3] BONTEMPS. A, GUARRIGUE.A, GOUBIER.C, HUETZ.J, MARVILLET.C, MERCIER.P, VIDIL.R ; Echangeurs de chaleur, Techniques de l’ingénieur, traité Génie énergétique, Références B2340, B2341, B2342, B2343, B2344.
[4] SHAH R.K.; Fundamentals of Heat Exchanger Design ; John Wiley & Sons, 2003.
[5] ROHSENOW W.M, HARTNETT J.P, CHO Y.I ; Hanbook of Heat Transfer ; 3rd Edition - McGraw-Hill, 1998, ISBN 0-07-053555-8
[6] Verein Deutscher Ingenieure (VDI) - Gesellschaft Verfahrenstechnik und Chemieingenieurwesen (GVC), Editor VDI Heat ATLAS 2nd Edition, Springer, 2010, ISBN 978-3-540-77876-9
[7] Standards of the Tubular Exchanger Manufacturers Association (TEMA), 9th Edition, 2007.
[8] CHAUDOURNE.S ; Les échangeurs à caloducs ; Collection « Echangeurs de chaleur », GRETh, Lavoisier TEC&DOC, Septembre 1987.
[9] BRICARD.A, CHAUDOURNE.S ; Caloducs ; Techniques de l’ingénieur, traité Génie énergétique, Référence b9545, Avril 1997.
[10] BRICARD.A, TADRIST.L ; Initiation aux échangeurs thermiques à contact direct ; Collection « Echangeurs de chaleur », GRETh & IUSTI, Lavoisier TEC&DOC, Juin 1996.
[11] BRICARD.A, TADRIST.L ; Echangeurs de chaleur à contact direct ; Techniques de l’ingénieur, traité Génie énergétique, Référence BE9565, Octobre 1999.
[12] H. DEMASLES, P. MERCIER, P. TOCHON, B. THONON - « Guide de l’encrassement des échangeurs de chaleur » (2007) Editions GRETH – ISBN : 2-9502555-5-8
[13] T.R. BOTT; Fouling of heat exchangers; Elsevier Science & Technology Books; April 1995, ISBN: 04444821864
[14] REAY.D.A, KEW. P.A, McGLEN.R.J; Heat Pipes – Theory, design and Applications, 6th edition, 2014, Elsevier, ISBN: 978-0-08-098266-3
[15] European Heat Exchanger Markets, #3752-17, Frost & Sullivan, 1999.
[16] Idel’cik – Mémento des pertes de charge, éditions Eyrolles, 1986

10. Sites Internet fournisseurs d’échangeur de chaleur (non exhaustif)

www.acm-acr.com	www.fivesgroup.com/FivesCryogenie	www.ravanat.fr
www.acte-sa.be	www.funke.de	www.sag-industries.com/fr
www.airec.se	www.guentner.com	www.sanhuamc.com
www.akg-group.com	www.hamon.com	www.sanhuamc.com
www.alfalaval.com	www.heatric.com	www.secanaerospace.com
www.allia-europe.com	www.howden.com	www.alpema.org
www.hrs-heatexchangers.com	www.serck-aviation.com	www.apiheattransfer.com
www.huber.fr	www.sglgroup.com	www.artic-industrie.com
www.kapp-process.com	www.sierra.it	www.atherm.com
www.kelvion.com	www.sissherbrooke.com	www.axintra.com
www.klingenburg.de	www.spirec.fr	www.balcke-duerr.com
www.kochheattransfer.com	www.spxflow.com	www.barriquand.com
www.labbe-france.fr	www.stiral.com	www.basetec.net
www.lennoxemea.com/fr/	www.swep.net	www.bisbrouck.fr
www.linde-engineering.com	www.calgavin.com	www.luvata.com
www.thermacore.com	www.caronetfils.com	www.luve.it
www.tmw-technologies.com	www.cepic.eu	www.tranter.com
www.trianon-echangeur.com	www.cetal.fr	www.lytron.com
www.chartindustries.com	www.mersen.com	www.quiri.com
www.ciat.com	www.cipriani-phe.com/?lang=fr	www.morgana.fr
www.vahterus.com	www.collardettrolart.com	www.motacoolingsystem.com
www.vdlklimafrance.com	www.danfoss.com	www.neotiss.com
www.vulcanic.com	www.wieland-thermalsolutions.com	www.ziemex.com
www.date.fr	www.deltaairplus.fr	www.faviersetrem.fr
www.nexson-group.com	www.occocoolers.co.uk	www.wlv.mfisupport.com
www.onda-it.com/fra/	www.phenomen-phe.com

11. Sites Internet fournisseurs de logiciel (non exhaustif)
www.htri.net
htfs.aspentech.com/
www.aspentech.com/products/aspen-edr
www.prosim.net/en/software-prosec-11
greth.fr/echtherm/
www.nist.gov/el/building_environment/evapcond_software

12. Sites Internet Association (non exhaustif)
www.nist.gov
www.tema.org
www.alpema.org
www.greth.fr